Cache Modeling: The Basics

The Basics

When I first started diving into computer architecture, I was fascinated by how modern processors manage memory.

When the CPU requests a memory address:

• It first checks - the cache(which sits very close to the CPU). If the data is found (a hit), it can be accessed quickly.

• If not (a miss), the CPU has to fetch the data from other "slower" memory(eg: RAM)

• This impacts performance as the CPU is sitting idle waiting for data.

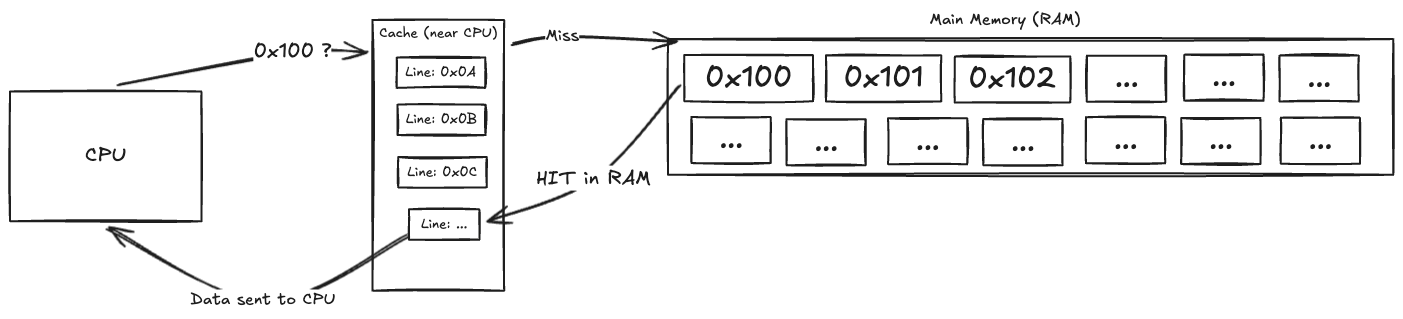
Another thing to note is that caches are smaller in size compared to main memory, so they can't hold all the data. Therefore, they use various strategies to decide which data to keep and which to evict when new data needs to be loaded. So the overall goal of any memory system or software optimization is to reduce the number of cache misses, and feed as much data as possible to the CPU, thereby improving performance.

AMAT

The number of cache misses/miss rate is a coarse metric to measure performance impact, a much better metric is the Average Memory Access Time (AMAT) because it takes into account the total time required to get that data - or in other words how much time the CPU is waiting for data(due to memory).

We can define, AMAT $= Hit\ latency + Miss\ ratio \times Miss\ penalty$

Let' say we have a cache with:

• Hit latency $= 2\ cycles$ ; Hit ratio $= 70\%$

and a Main memory with, Access Latency $= 30\ cycles$

Now going by the equation above, we can calculate AMATfrom the cache prespective

$= 2 + (1 - 0.7) \times 30$ $= 11 \ \text{cycles}$

Modern CPUs have multiple levels of cache (L1, L2, L3), L1 being the smallest and fastest, and L3 being larger and slower. One can say that in terms of speed(access time):

$= Disk > RAM > L3 > L2 > L1 > CPU Registers$

in terms of size

$= CPU Registers < L1 < L2 < L3 < RAM < Disk$

On windows you can actually check this for yourself using the Task Manager^[1]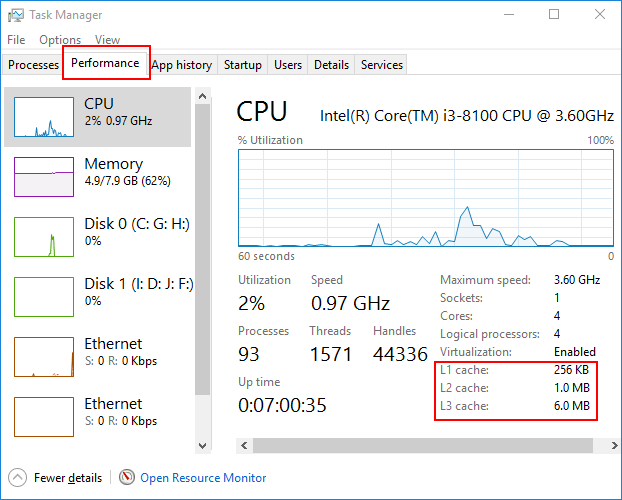

Let's try to use the AMAT equation assuming that we have:

• L1 cache from eqn 1 -> Hit latency $= 2\ cycles$ ; Hit ratio $= 70\%$

• L2 cache with: Hit Latency: $= 5\ cycles$ ; Hit ratio $= 90\%$

• the same main memory with: Access Latency $= 30\ cycles$

$AMAT_{L2} = 5 + (1 - 0.9) \times 30$ $= 8 \ \text{cycles}$

Now let's substitute the miss penatly for L1 as $AMAT_{L2}$

$AMAT_{L1} = 2 + (1 - 0.7) \times 8$ $= 4.4 \ \text{cycles}$

We see that AMAT has reduced from 11 cycles to 4.4 cycles by adding an additional cache level, which is a significant improvement.

Cache Mapping Techniques

How a cache maps data from main memory to the cache is determined by its mapping technique. There are three common techniques:

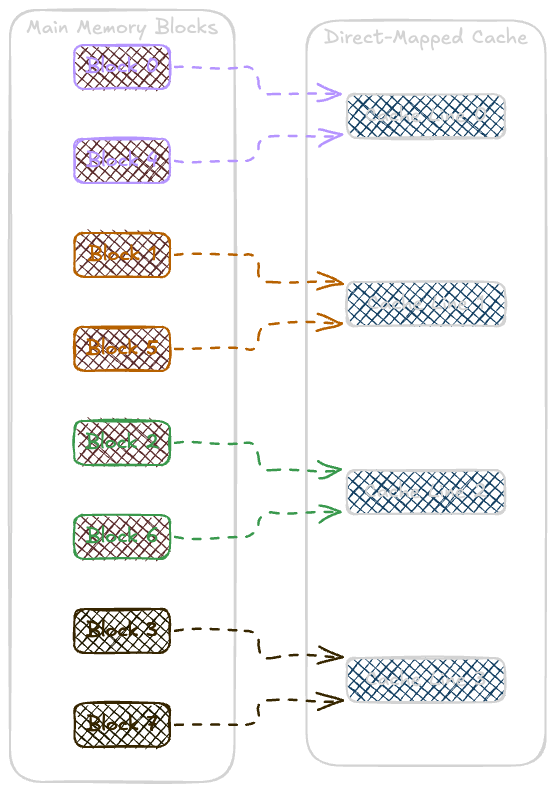
1. Direct-Mapped Cache: Each block of main memory maps to exactly one cache line. This is simple but can lead to many conflicts and cache misses.

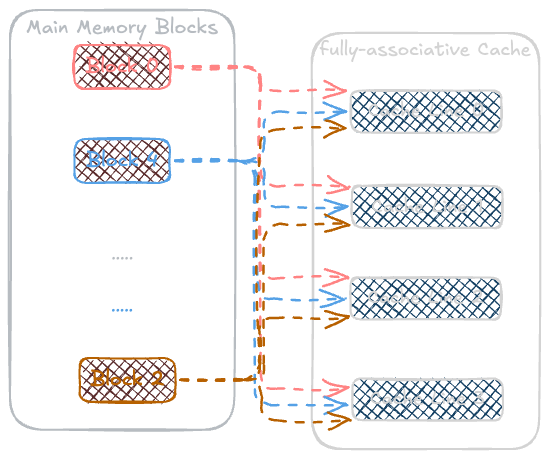
2. Fully Associative Cache: Any block of memory can be placed in any cache line. This offers the most flexibility but is more complex and expensive to implement.

3. Set-Associative Cache: The cache is divided into sets, and each block of memory can map to any line within a specific set. This reduces conflicts compared to direct-mapped caches. ways are basically the number of cache lines in a set

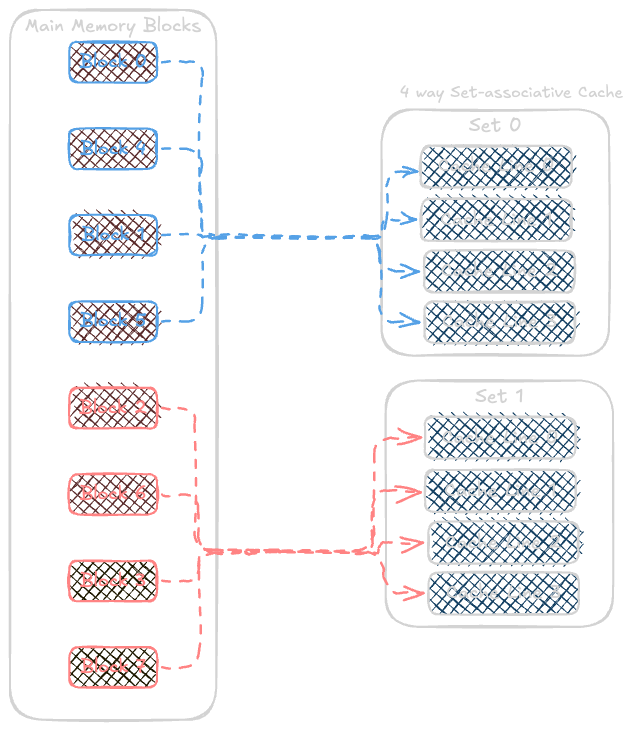
Cache Specific Parameters

Apart from having different cache levels, there are cache specific parameters like:

• Cache Size: Larger caches can store more data, which can reduce the number of cache misses. However, larger caches are also more expensive and can have longer access times.

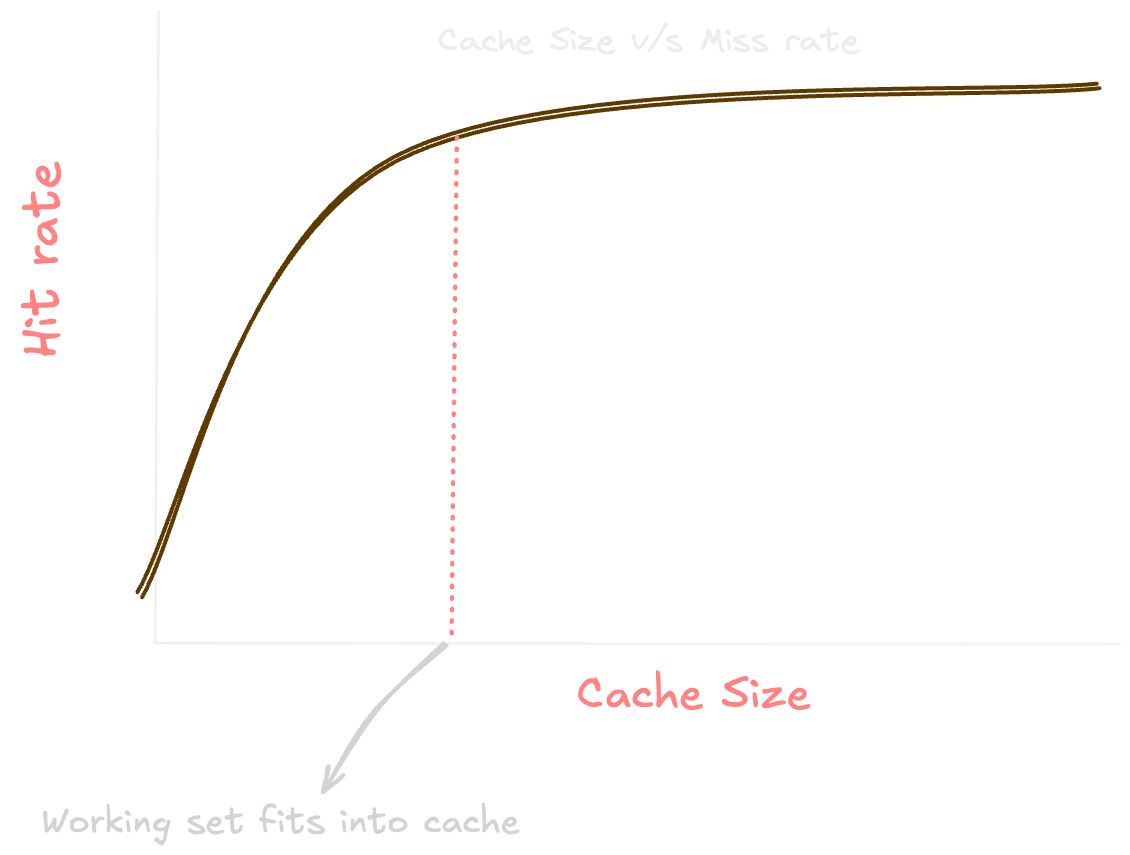
• Block Size: This is the amount of data that is transferred between the cache and main memory in a single operation. Larger block sizes can take advantage of spatial locality, as accessing one part of a block often means that nearby data will also be accessed soon. However, larger blocks can also lead to more cache misses if the data being accessed is not contiguous.

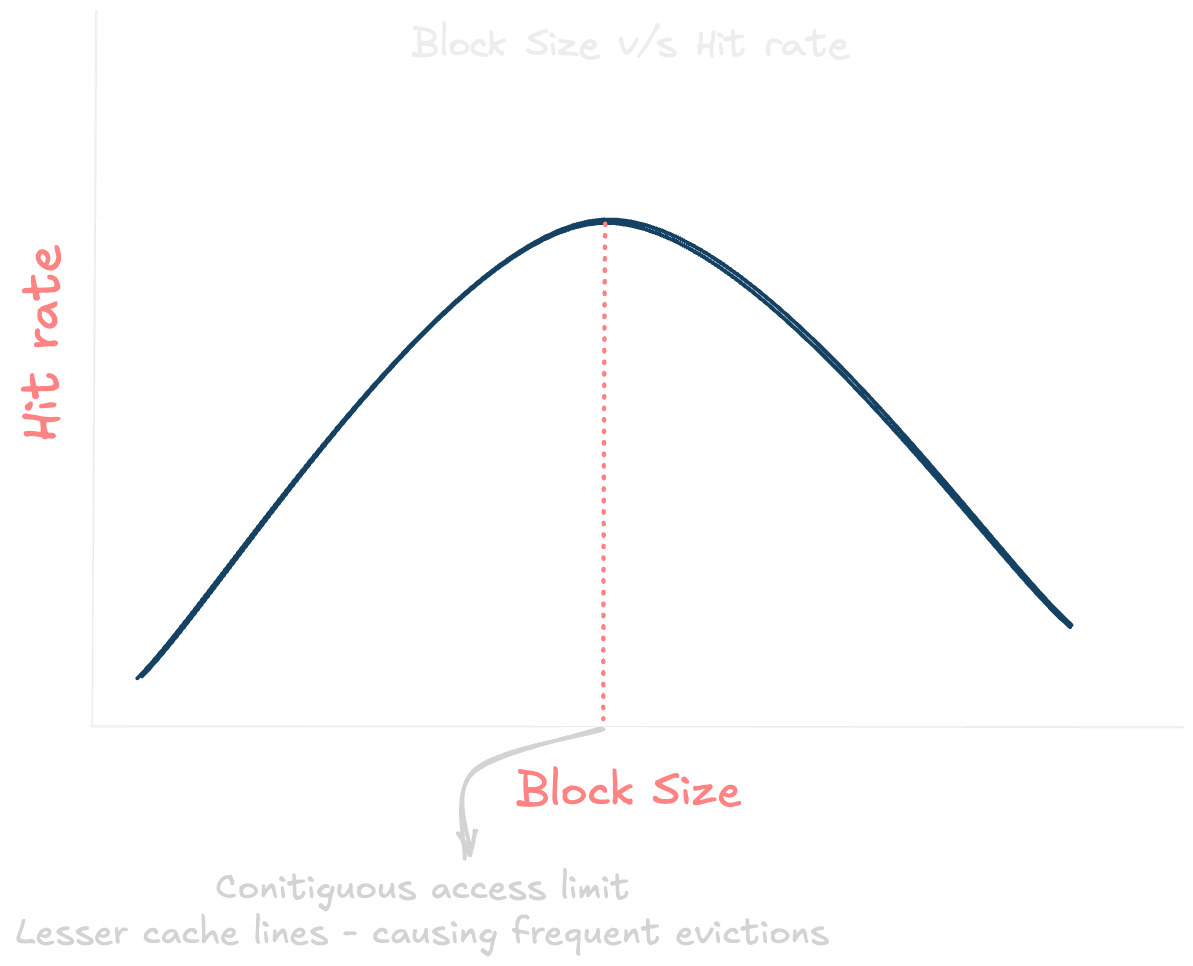
• Associativity: This refers to how many places in the cache a particular block of memory can be stored. Higher associativity generally leads to fewer cache misses, as there are more options for where to place data within the cache. However, higher associativity also increases the complexity and cost of the cache.

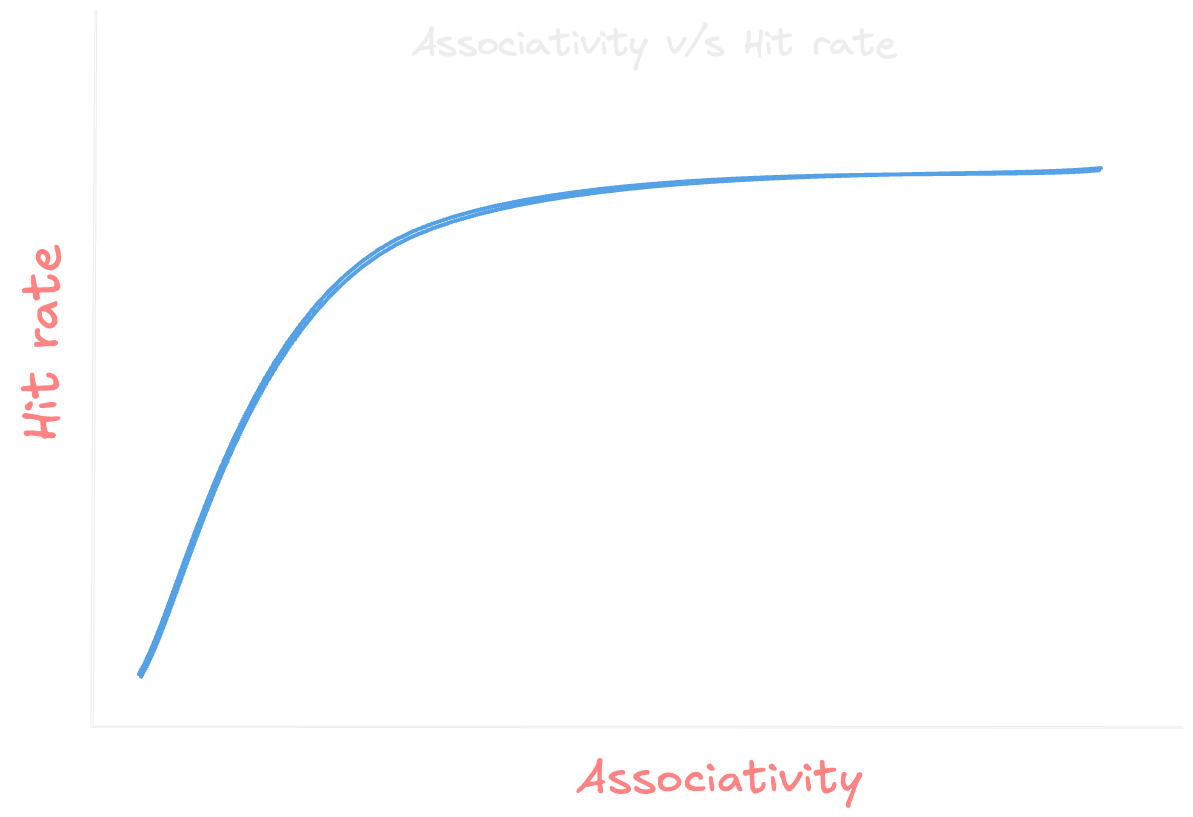
I think it's a good time to stop here, as we have covered the basics of cache memory, its hierarchy, and some important parameters that affect its performance.

The next blog talks about implementing all of the above using C++.

[1]	In a multi-core CPU, the L3 cache is usually shared among all cores, while L1 and L2 caches are typically private to each core.